Hoewel optiegrieken voor beginnende beleggers soms complex kunnen lijken, zijn ze essentieel bij het begrijpen en beheren van risico’s in de optiemarkt.
In dit artikel gaan we dieper in op de optiegriek gamma. U leert wat gamma precies inhoudt, hoe het zich gedraagt onder verschillende marktomstandigheden en wat de implicaties zijn voor uw handelsstrategieën.
Opties zijn complexe financiële instrumenten en brengen aanzienlijke risico’s met zich mee. Beleggers moeten zorgvuldig overwegen of ze geschikt zijn voor hun beleggingsdoelstellingen en risicobereidheid. Beleggers moeten ook hun kennis van de optiemarkt en verschillende strategieën vergroten voordat ze beginnen met handelen in opties.
Gamma betekenis
Gamma meet de verandering van de delta bij een koersverandering van de onderliggende waarde.
Eerst even als opfrissing: de delta van een optie geeft aan met hoeveel de waarde van een optie verandert bij een verandering van één punt in de onderliggende waarde. Gamma daarentegen meet hoe snel die delta zelf verandert als de onderliggende waarde beweegt.
Wanneer de onderliggende waarde met één eenheid stijgt, dan neemt de delta toe met de waarde van gamma. Daalt de onderliggende waarde met één eenheid, dan daalt de delta met dezelfde gamma. Gamma geeft dus inzicht in de gevoeligheid van delta – een hoge gamma betekent dat de delta snel verandert bij bewegingen in de markt, terwijl een lage gamma wijst op een stabielere delta.
Hieronder geven we u een voorbeeld om duidelijk te maken wat de impact is van de optiegriek gamma.
We bekijken drie verschillende call opties op de AEX-index met strike 565, 570 en 575. De huidige stand van de Nederlandse index was destijds 572. De gamma van de 565 strike is 0,018, terwijl de delta 0,645 is. Mocht de AEX-index stijgen naar 573, dan zou de theoretische waarde van de delta van de call 565 moeten stijgen naar 0,663 (delta + gamma = 0,645 + 0,018). U kunt nu zelf de berekening maken bij eenzelfde waardestijging in de index, voor de call optie strike 570 en 575. Er zou een nieuwe delta moeten uitkomen van 0,465 voor strike 575 en 0,572 voor strike 570.
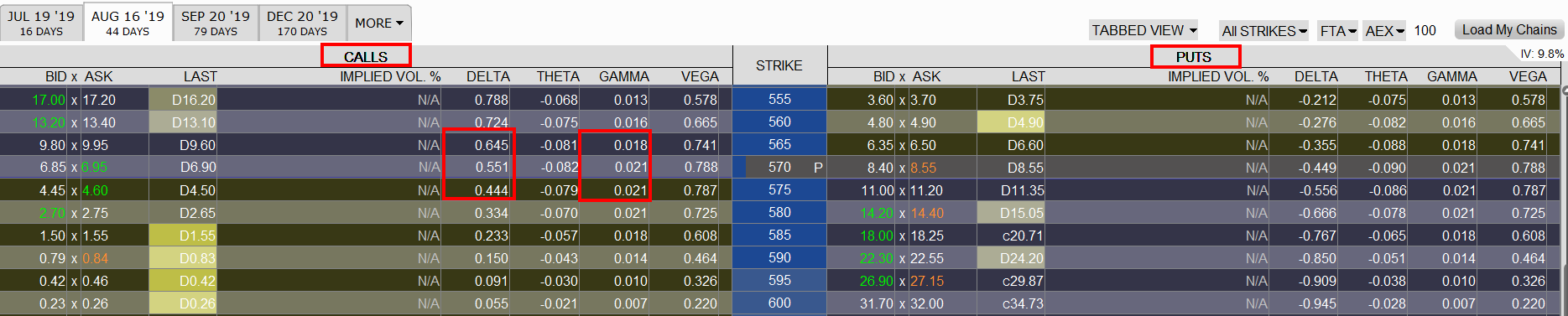
Eigenschappen van gamma
Gamma is altijd positief voor gekochte opties (zowel calls als puts). Wanneer u opties schrijft, is de gamma negatief – wat betekent dat veranderingen in delta in uw nadeel kunnen werken.
Aandelen en opties:
Indien u ons andere artikel over de delta heeft gelezen, dan weet u dat een positie in de onderliggende waarde gelijk staat aan 1 delta. Bijvoorbeeld:
- Een long aandelenpositie van 100 aandelen Apple komt overeen met delta 1
- Een short aandelenpositie van 100 aandelen Facebook komt overeen met delta -1
Deze delta’s in het bovenstaande voorbeeld blijven constant. Dat wil zeggen dat bij een long of short aandelenpositie de gamma gelijk is aan nul. Er vindt namelijk geen verandering in de delta plaats.
Risico-indicator:
Een hoge gamma, zowel positief bij long opties als negatief bij short opties, betekent een hoog risico. Een lage gamma betekent een lager directioneel risico. Indien u deltaneutraal bent met uw positie, maar tegelijkertijd een zeer hoge gamma heeft, betekent dit dat uw niet directionele positie wel eens sterk directioneel zou kunnen worden.
Maximale gamma:
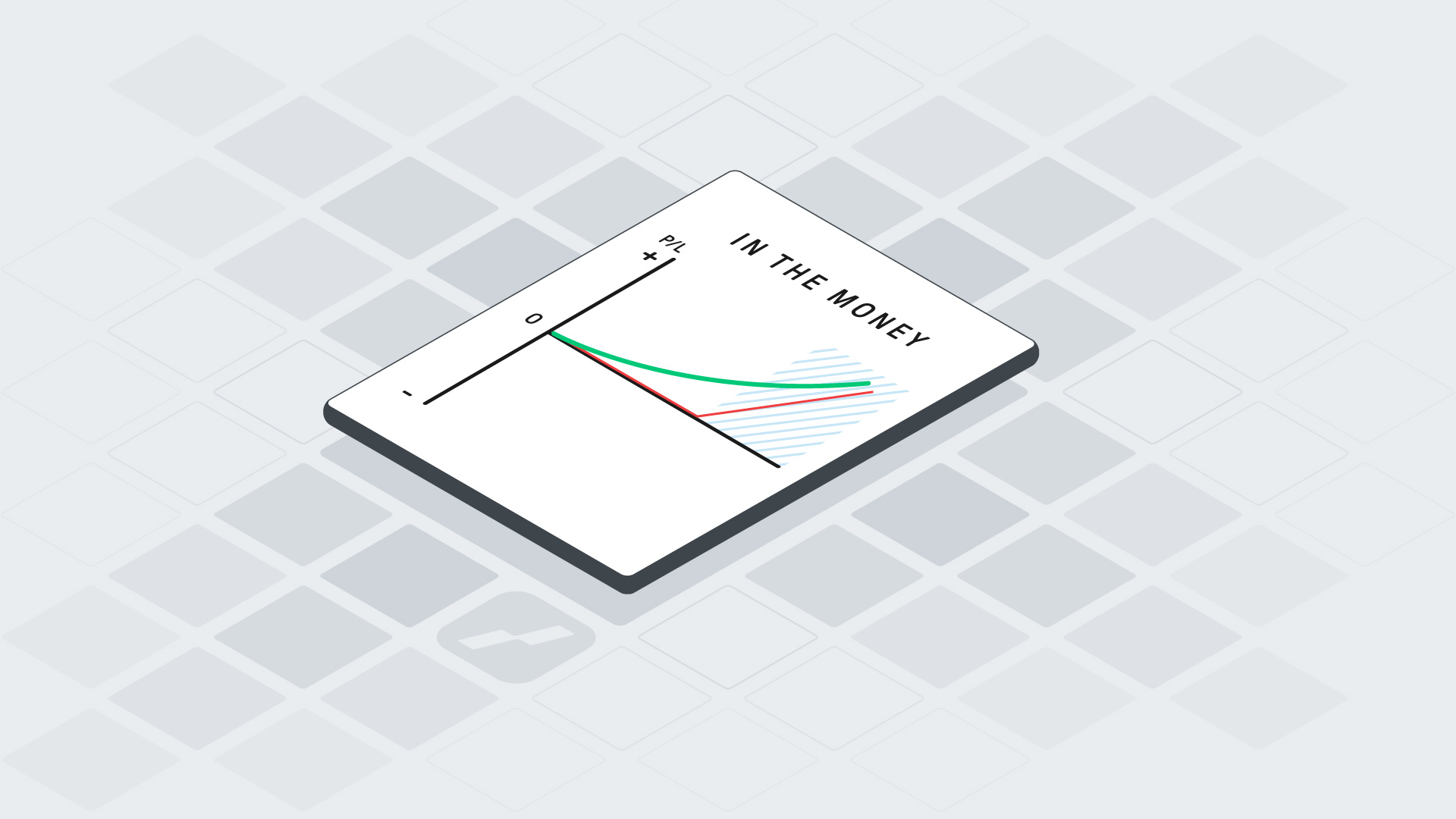
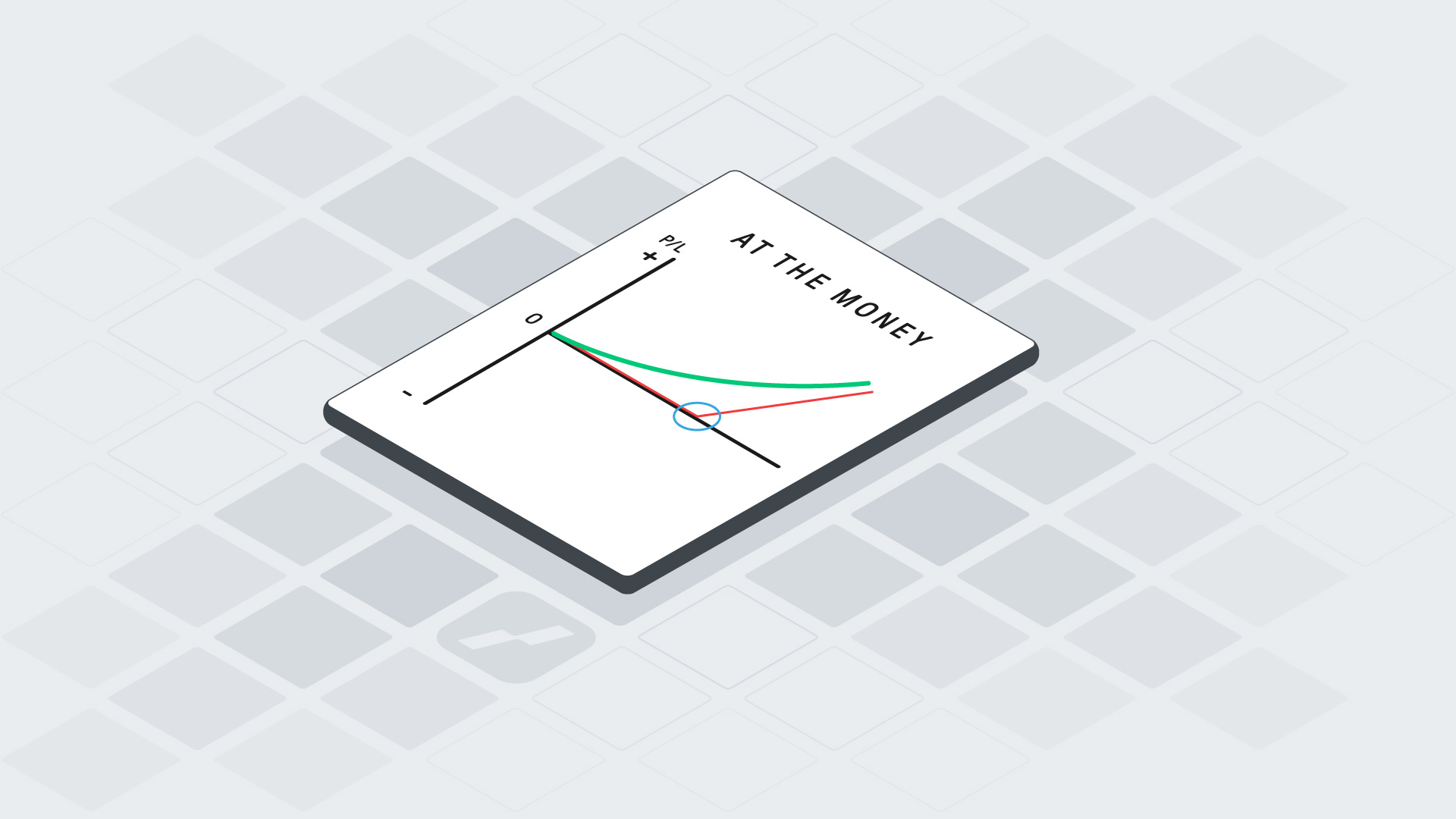
Gamma bereikt zijn hoogste waarde bij opties die at-the-money zijn. Bij deep in-the-money of far out-of-the-money opties is gamma doorgaans laag, omdat de delta in die gevallen nauwelijks nog verandert bij kleine koersbewegingen. Hieronder een voorbeeld om het duidelijk te maken:
Illustratie: gamma rond de AEX 570
Stel: de AEX staat op 570. Een diepe in-the-money call heeft een delta dicht bij 1. Deze zal bij een stijging van de index weinig extra delta opleveren, waardoor de gamma laag is. Bij een at-the-money call is de delta circa 0,5 – bij een stijging van de onderliggende waarde stijgt deze delta aanzienlijk sneller, en dus is gamma daar hoger. Out-of-the-money calls starten met een lage delta, en hun gamma is vaak beperkt.
U kan op basis van de onderstaande afbeelding het bovenstaande verhaal volgen. In onderstaande voorbeeld is voor alle duidelijkheid:
- Strike 570 = At-the-money = ATM
- Strike 530 = In-the-money = ITM
- Strike 605 = Out-the-money = OTM
Impact gamma op de optieprijs
Wanneer u als belegger de optiegrieken onder de knie heeft, kunt u een klein beetje in de theoretische toekomst kijken en zo uw risico beter in de hand houden. Hieronder vindt u een uitgewerkt voorbeeld:
In dit voorbeeld maken we gebruik van de AEX index. De stand van de AEX was in deze situatie 567,86. Een call 565 aug 16 ’19 noteert aan 7,5, heeft een delta van 0,555 en een gamma van 0,019.
Stel dat de prijs van de AEX van 567,86 naar 568,86 gaat, dan weten we dat de optieprijs theoretisch gezien zou moeten stijgen naar 8,055 (7,50 + 0,555). De delta geeft namelijk weer wat de prijswijziging is van de optieprijs, wanneer het onderliggende wijzigt met 1 eenheid.
In dit voorbeeld zien we ook dat de gamma 0,019 is. Zoals uitvoerig besproken in dit artikel zegt de gamma iets over de wijziging in de delta wanneer het onderliggende wijzigt met 1 eenheid. Als de prijs van de AEX stijgt naar 568,86, dan zou de nieuwe delta van de besproken optie theoretisch gezien 0,574 worden (0,555 + 0,019).
Stel dat de prijs van de AEX van 567,86 naar 566,86 gaat, dan weten we dat de optieprijs theoretisch gezien zou moeten dalen naar 6,945 (7.5-0.555). De delta geeft namelijk weer wat de prijswijziging is van de optieprijs, wanneer het onderliggende wijzigt met 1 eenheid.
| Prijs AEX-index | Optieprijs | Delta | Gamma |
| 568.86 | 8.055 | 0.574 | / |
| 567.86 | 7.50 | 0.555 | 0.019 |
| 566.86 | 6.945 | 0.536 | / |
Hieronder ziet u een overzicht van de verhouding tussen delta en gamma ten opzichte van een directionele positie:
| Directionele positie | Delta | Gamma |
| Long call optie | + | + |
| Short call optie | – | – |
| Long put optie | – | + |
| Short put optie | + | – |
| Long aandelenpositie | + | 0 |
| Short aandelenpositie | – | 0 |
De relatie tussen gamma en volatiliteit
Gamma wordt beïnvloed door volatiliteit, wat belangrijk is om te weten bij het kiezen van strategieën:
Lage volatiliteit:
- Gamma van ATM-opties stijgt
- Gamma van ITM- en OTM-opties daalt
Hoge volatiliteit:
- Gamma van ATM-opties daalt
- Gamma van ITM- en OTM-opties stijgt
De gamma van een call en put met gelijke strike en looptijd is identiek.
Naarmate de expiratie dichterbij komt, stijgt de gamma van At-the-money opties doorgaans sterk.
Verder leren? Ontdek andere optiegrieken
De gamma is één van de vier belangrijkste optiegrieken. In ons artikel over de optiegriek delta leggen we uit hoe hoeveel de theoretische waarde van de optie verandert bij een wijziging van één punt in de onderliggende waarde.
Bent u nieuw met opties? Lees dan eerst het artikel: ‘Wat zijn opties en hoe kunt u beleggen in opties?’, die u de basis uitlegt van A tot Z.
Gamma optiegriek gebruiken bij het handelen via LYNX?
Via LYNX kunt u zeer voordelig beleggen in opties. Met enkele muisklikken handelt u eenvoudig in alle Europese en Amerikaanse aandelenopties en indexopties. Tevens heeft u de beschikking over geavanceerde Trader Tools zoals de OptieTrader en kunt u optiecombinaties in zijn geheel naar de beurs versturen.
